

Ever see someone demonstrate lift by blowing over a piece of curved paper? While this is fun and interesting, the usual explanation given is mistaken; claiming it’s an effect of the Bernoulli principle, the correlation between air speed and pressure. As fluid flow speed increases static pressure decreases. That is, the air (or any gas or liquid) is less dense, there is more space between particles. Many folks were taught this is how planes fly, and they pass this “wisdom” along. But they’re fooling themselves, and you.
Aerodynamic engineers have know the correct explanation of lift for decades, yet the misconception of Bernoulli principle lift lives on in the public imagination. However, it is not how an airfoil generates lift. That’s a whole different kettle of fish. (See links at bottom.)
By the way, the illustrations and animations here are not true diagrams or any kind of proof, just visual aids. Fluid behavior is a complicated business which can seem like organised chaos, what with tumbling and swirling, i.e., turbulence. We’re not going to get into these details, but concentrate on simplified basics. (Besides, animation can show the impossible, like walking on air and not falling until you look down.)
What does this correlation between speed and pressure mean? Here’s a way to imagine it. Say you have two lanes of traffic, one fast and one slow. The little men waiting at the crosswalks each see one car per second go by. They each see the same number of cars in the same time, but the gaps between the cars are bigger in the faster flow below. The traffic is less dense the faster it goes.
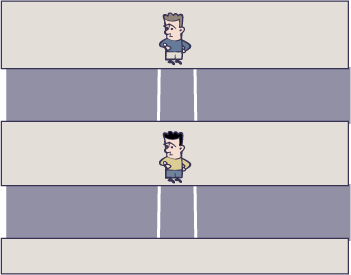






This is basically what the Bernoulli principle is about, only with liquids and gasses, not cars. The faster the air flows the more it gets stretched out so there’s less air in the same volume, it’s less dense, static pressure is lower. As speed increases pressure decreases, and vice-versa.
Higher speed also means more force in the direction of flow, which is called dynamic pressure. For instance, if the little men step into the road the bottom guy will take a bigger hit from a fast car than will the top guy from a slower car. You consider only static pressure and ignore dynamic pressure at your peril. Which is what happens with certain misleading demonstrations or mistaken explanations of lift.
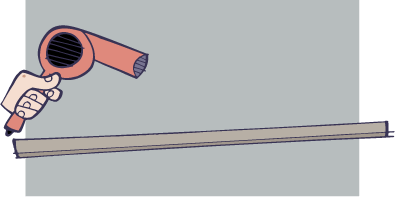
Paper Lift: Let’s have a look at a the lift demonstration mentioned in the opening and see what it’s about. Take a piece of stiff paper and curve it like a wing. Put a tab of tape on the end to act as a hinge and blow a stream of air over it. It lifts!


The common explanation given says the fast airstream over top has lower pressure, as per the Bernoulli principle, which sucks the paper up. Sounds plausible, but there’s a problem with it which we’ll get to below.
Converging Cans: There are many variations of this, but here’s one I did. Place two empty cans spaced about three inches apart on a table up against a flat strip of wood so they won’t blow away. Blow a fast stream of air between them and they move together. (In the animation they return to start when the stream stops, but that’s just to reset things. They won’t do that on their own in real life.)



The explanation usually provided for this phenomenon is by speeding up the air between the cans you reduce the pressure in the airstream as per the Bernoulli principle. The lower pressure pulls the objects into the stream so they come together.
Unfortunately, there’s a problem. Here’s how to show it. Attach a piece of stiff paper to each can and set them up the same as before with the paper making a parallel channel. Blow air between them and… they don’t move. In fact, they may move apart a bit.




The problem with both “lift” demonstrations is not noticing the airstream is flowing across a curved surface. This makes a big difference, as we can see by changing the shape of the cans from rounded to flat-sided. When the surface isn’t curved you don’t get the movement. The Bernoulli effect doesn’t work in that case. Why? Because it wasn’t the Bernoulli priciple causing the “lift” in the first place. It was the Coandă effect.
The Coandă effect is about how a fluid (gas or liquid) attaches to and flows across a surface. In our particular case, a curved surface. You’ve no doubt made a puddly mess as the result of this effect in everyday life without knowing what it’s called or who to blame.

Take a glass filled with grape Kool-Aid (any flavor will do) and slowly tip it so the liquid starts to spill out. Notice it sticks to the glass, running down the side and dribbling off the bottom. The fluid flow attaches to the side of the glass surface defying gravity. (This is not because of surface tension, despite what everyone on This Old House seems to think. To avoid this sort of thing is why pitchers have spouts. But we’ll not go into that now.)
Something along those lines is what’s happening in the demonstrations given above. The air sticks to and flows along the curved surface and bends matching the curved shape. That’s what creates the “lift,” not the change in static pressure.
You can easily demonstrate the Coandă lift effect for yourself with a tablespoon and faucet. These are conveniently often found together in the kitchen, no need for highly technical lab equipment. Follow the steps given below. Gases behave pretty much like liquids, so when you see the water behaving strangely with the spoon, that’s what the air does with the curved paper.
Dangle the spoon as shown next to the stream coming from the tap. I say dangle because you want to hold it loosely enough so it can swing back and forth a bit like a pendulum. (It helps to attach a piece of tape at the handle end to act as a hinge.) Move the spoon up to the edge of the stream so it barely touches. When you do the water will flow around the bowl of the spoon and off the bottom deflected to the side and the spoon will swing into the stream.


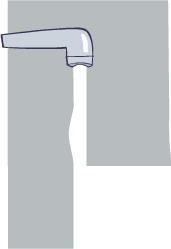

Just as water flowing around the spoon’s curved surface draws it into the stream, air blown around the curved paper or round cans is what causes the movement in those cases. You wouldn’t know it by looking at it because you can’t see the flow of air like you can see the flow of water. What we have is circular motion, or partial circular motion, but the forces at work are the same. To understand how a curving airflow creates this lifting action, we must first understand circular motion.
Circular motion is the result of combining linear momentum and a centripetal force at a right angle to the momentum. In the following animation the ball’s momentum (white arrow) is from left to right until it reaches and sticks onto the rod attached to an axle. The rod is a centripetal force (black arrow) at a right angle to the ball’s momentum from the tip toward the axle. As the ball continues its motion it is continually deflected resulting in circular motion until it detaches and flies off straight.

The result of circular motion is a centrifugal effect, a reaction force in the opposite direction of the centripetal force, away from the axle. So, if the ball attaches to the rod near the axle, when the rod rotates the ball travels along the rod outward away from the hub due to centrifugal effect (red arrow). If the ball is stopped at the end of the rod the centrifugal effect is still there tugging outward on the rod trying to pull it away from the axis. Once detached there is no longer either centripetal or centrifugal force on the ball, it flies off straight.

All the above applies whether something is moving in a full circle or only part of a circle. Let’s say the ball flies in and attaches to the rod as before. Only this time it detaches after a quarter turn. Meaning the centripetal and centrifugal forces are only there during the partial circle, along the arc, on the curve, in the turn.

Now let’s look at the same thing with an invisible rod and a stream of balls showing only the centrifugal force arrow. Notice how the arrows seem to only point generally upward? Up, that’s the same direction as lift. Is it starting to look similar to something we’ve seen before? Say, the paper lift or spoon?

Just like in the demonstrations, where the flow of air or water is curving there is centrifugal effect on that flow in the direction opposite the bending. For instance, where the water is bending around to the right, there is a centrifugal effect to the left. Just as the water is attached to the spoon, the spoon is attached to the water and so the centrifugal affect is on both. That’s what makes the spoon move left. And the paper lift, and the cans move together. (Admittedly the can animation cheated by not showing the airstream curling around the cans. I just didn’t know how to animate that easily.)
We repeat the faucet demo below showing the forces described above as they apply in this case. As before, the white arrow is momentum, the black arrow is the centripetal force of attachment on the flow from the spoon causing the flow to curve. The red arrow is the resulting centrifugal effect on both the water and the spoon generating the “lift” so the spoon stays swung to the left.


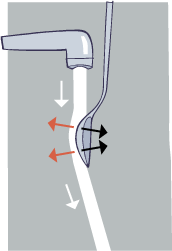
Notice how unlike a wing in flight everything we’ve look at is, flow on one side only. The Coandă effect only works in specific conditions where an isolated jet of fluid flows across a surface. This doesn’t happen with a wing as there’s airflow both above and below. Just so you know, there is practically no Coandă lift on an airfoil. And very little Bernoulli effect lift, too.
There are other factors in the Coandă effect, such as why the flow attaches to the surface, shear, laminar flow, total pressure, entrainment; but what’s given above is the prime factor in the lifting effect. How exactly it all works is unimportant to basic understanding. Do the spoon test and you’ll see that it works. I can’t explain gravity either, but we both know it’s real enough.
There are many other flying related phenomena misattributed to the Bernoulli principal, but those will have to wait until I feel more ambitious.
Still, after all is said and done you can always count on increased air speed to reduce pressure as described by the Bernoulli principle. However, once it encounters a new force, like a wall, curved surface, or you sitting there being cooled off, additional principles also apply and might have more effect. How a fan cools you is another can of worms we won’t go into. But I will say this, it has nothing to do with the Bernoulli principle or the Coandă effect. At least, I’m pretty sure it doesn’t. I’ll look into it later.
© Terry Colon, 2018
The Coandă effect is named for Romanian air pioneer Henri Coandă, an interesting character in his own right. He built and flew the first proto-jet plane in 1910.
Henri Coandă –biography
The Coandă 1910 –the First Jet
Special thanks to fluid dynamics engineer Terry Day whose invaluable assistance, and patience, helped me understand it. His site:
Other bits from the flying files:
A Simple Way to See How Planes Fly
The Trouble with Airflow Diagrams
If you tuned in for our how planes fly bits, you might like our take on bicycles: